Theory: Traversal

A step-by-step search of tree elements by links between ancestor and descendant nodes is tree traversal. We assume that each node will be affected only once during the crawl. By and large, everything is the same as in traversing any collection using a loop or recursion.

However, in the case of trees, there are more ways of traversing than just left to right and vice versa.

Depth-first traversal is the only traversal order we will use in this course because it naturally follows from recursive traversal. You can read about the rest of the methods in Wikipedia or the books recommended by Hexlet.

Depth-first search

It is one of the tree traversal methods. The strategy of this search is to go as deep into one subtree as possible. This algorithm naturally falls on a recursive solution and works itself out naturally:

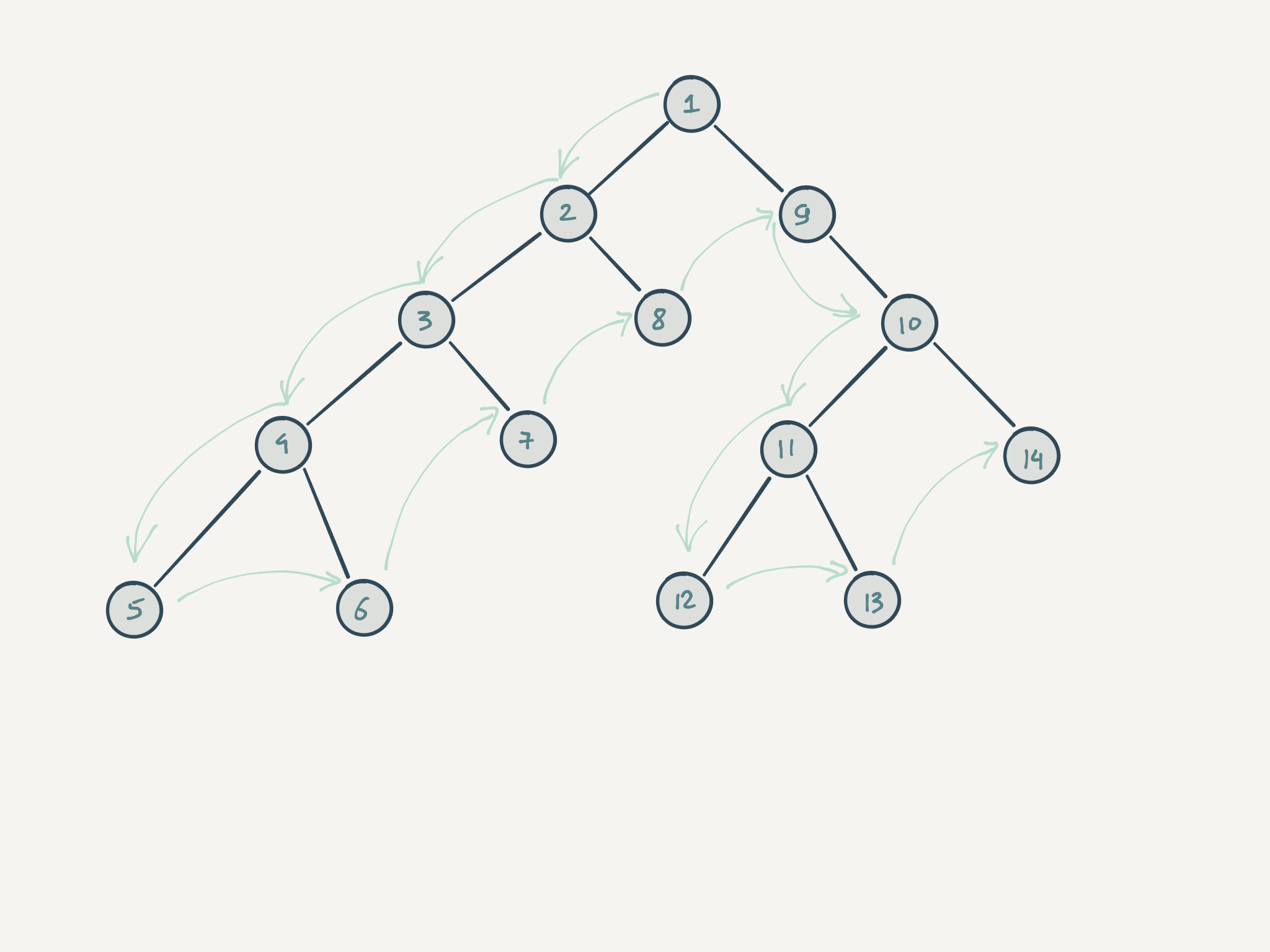
Let's look at this algorithm using the following tree as an example:

#     * A
#   / | \
# B * C * D
#  /|   |\
# E F   G J

We indicate each non-leaf node by an asterisk. The crawl starts from the root node:

1. Check if node A has children. If there is, then we run the traversal recursively for each child independently

2. The next subtree is inside the first recursive call:

   # B *
   #  /|
   # E F

   Expand code

   We repeat the logic of the first step and fall to the level below.

3. There is a leaf element E inside. The function makes sure that the node has no child elements, performs the necessary work, and returns the result to the top

4. We find ourselves in this situation again:

   # B *
   #  /|
   # E F

   Expand code

At this point, we launched a recursive call on each of the children. Since we have already visited the first child, the second recursive call goes to node F and does its job there. After that, it's returned to the top, and everything repeats until it reaches the root:

from hexlet import fs

tree = fs.mkdir('/', [
    fs.mkdir('etc', [
        fs.mkfile('bashrc'),
        fs.mkfile('consul.cfg'),
    ]),
    fs.mkfile('hexletrc'),
    fs.mkdir('bin', [
        fs.mkfile('ls'),
        fs.mkfile('cat'),
    ]),
])


def dfs(node):
    # Printing the name of the node
    print(fs.get_name(node))
    # If it is a file, we return control
    if fs.is_file(node):
        return

    # Getting children
    children = fs.get_children(node)
    list(map(dfs, children))

When we apply the dfs function to all children, we get a tree recursion — multiple recursive calls within a single function call:

dfs(tree)
# => /
# => etc
# => bashrc
# => consul.cfg
# => hexletrc
# => bin
# => ls
# => cat

Printing to the screen in the example above is just a demonstration. In reality, we want to change the tree or aggregate data. We'll consider data aggregation later, but now we'll analyze the change. Let us say we want to implement a function that changes the owner for the entire tree with all directories and files. To do this, we will combine two things:

• The recursion discussed above
• The node update code that we studied in the last lesson

Here is the code:

import copy
from hexlet import fs


def change_owner(node, owner):
    name = fs.get_name(node)
    new_meta = copy.deepcopy(fs.get_meta(node))
    new_meta['owner'] = owner
    if fs.is_file(node):
    # Returning the updated file
        return fs.mkfile(name, new_meta)
    children = fs.get_children(node)
    # This is the key line
    # Calling a recursive update of each child
    new_children = list(map(lambda child: change_owner(child, owner), children))
    new_tree = fs.mkdir(name, new_children, new_meta)
    # Returning the updated directory
    return new_tree

# We can generalize this function to a map that works with trees

The key difference from the first example is that we form new nodes and return them outside here instead of printing to the screen. Eventually, we assemble a new tree from them. Everything we will do further during the course is based on this algorithm. Try to open the editor on your computer and implement this function to be sure you understand what is happening.