Operations on sets — Python: Dictionaries and Sets

• Checking sets for equality
• Combining sets
• Checking intersections of sets
• Checking differences between sets
• Checking symmetric differences
• Checking subsets and supersets

You've already learned how to create and modify sets. But if we limit ourselves to that, it might seem that sets aren't all that different from lists. Yes, they allow you to check if an item exists more quickly, but they do not support slices. So the richness and power of comparing sets bring the benefit.

Checking sets for equality

Let's check two sets for equality:

set([1, 2, 3, 2, 1]) == {3, 1, 2}  # True

You might think two sets are the same if the second set contains every element of the first one, and your guess would be close to the truth. But remember that collections in Python only store references to objects. So are sets equal if they point to the same objects? Identical references are equal, that's true, but different objects can also be equal.

The fact is that Python has a special equality-checking protocol. Most of the embedded data types support this protocol. We can check the equality of numbers, strings, and boolean values. And we can also make tuples, lists, and dictionaries equal. And that's where Python is good. When we equate two collections of the same type, we consider those collections equal if their elements are equal pairwise (again, from a protocol point of view). Take a look:

[1, 2, ["foo", "bar"]] == [1, 2, ["foo"] + ["bar"]]  # True
(1, True, []) == (1, True, [])  # True
{"a": 1, "b": 2} == {"b": 2, "a": 1}  # True

Dictionaries are equal if the order of the keys is different. The sets of keys themselves are the same as long as the values for the corresponding keys are the same. So sets are equal if they contain identical sets of equal elements in pairs.

Combining sets

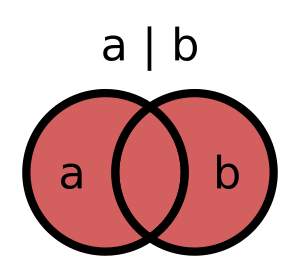
Sets in Python, like in mathematics, support the union operation. This operation does not combine sets, as it might seem, but returns a new set. It is an object containing all the items from at least one of the original sets.

In terms of meaning, the union operation is similar to the OR operation in Boolean logic: an element is present in the union set if it is present in the first source set OR in the second. Python uses the | operator to join sets:

visited_by_masha = {'Paris', 'London'}
visited_by_kolya = {'Moscow', 'Paris'}
visited_by_kolya | visited_by_masha  # {'London', 'Moscow', 'Paris'}

Checking intersections of sets

If there is an operation similar to OR, then it would be logical to assume that there is also an "AND" operation. Yes, there is, called the intersection of sets.

The intersection involves elements that are present in both the first of the original sets and the second. The intersection operator is &. Here's an example:

visited_by_masha = {'Paris', 'London'}
visited_by_kolya = {'Moscow', 'Paris'}
visited_by_kolya & visited_by_masha  # {'Paris'}

Checking differences between sets

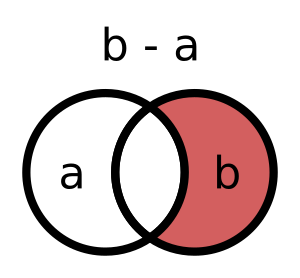
The difference of a pair of sets is a set whose elements are contained in the first original set but not in the second. We represent the difference by the - operator (similar to subtraction in arithmetic). Here is an example:

visited_by_masha = {'Paris', 'London'}
visited_by_kolya = {'Moscow', 'Paris'}
visited_by_masha - visited_by_kolya  # {'London'}
visited_by_kolya - visited_by_masha  # {'Moscow'}

Checking symmetric differences

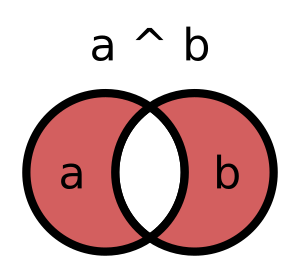
A symmetric difference is a set containing elements present in EITHER the first OR the second original set. The operation is similar to exclusive OR (XOR), so we represent it by the ^ operator. Here is an example:

visited_by_masha = {'Paris', 'London'}
visited_by_kolya = {'Moscow', 'Paris'}
visited_by_kolya ^ visited_by_masha  # {'London', 'Moscow'}

Checking subsets and supersets

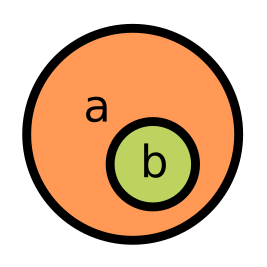
One set is a subset of another if the second contains all the elements of the first one, but the second may also have other elements. The second set is then a superset of the first.

We can check this relationship between sets with the issubset and issuperset methods:

a = {1, 2, 3, 4}
b = {3, 4}
b.issubset(a)  # True
a.issuperset(b)  # True

Fun fact: equal sets simultaneously are both subsets and supersets for each other.